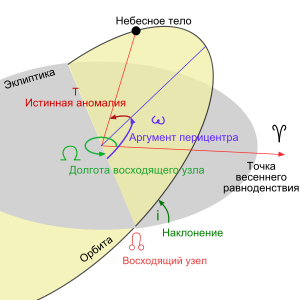
Кеплеровы элементы орбиты
Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:
- большая полуось (),
- эксцентриситет (),
- наклонение (),
- долгота восходящего узла (),
- аргумент перицентра (),
- средняя аномалия ().
Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию плоскости орбиты по отношению к базовой плоскости, шестой — положение тела на орбите.
В случае если орбита является эллипсом, его большая полуось положительна[1] и равна половине длины большой оси эллипса, то есть половине длины линии апсид, соединяющей апоцентр и перицентр эллипса[1][2][3].
Определяется знаком и величиной полной энергии тела: [3]. Связана с положением и скоростью тела соотношением , где μ — гравитационный параметр, равный произведению гравитационной постоянной на массу небесного тела[1][2].
Эксцентрисите́т (обозначается « » или «ε») — числовая характеристика конического сечения. Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия[4]. Эксцентриситет характеризует «сжатость» орбиты. Он выражается по формуле:
- , где — малая полуось (см. рис.2)
В зависимости от величины орбита представляет собой[1][2][3][5]:
- — окружность
- — эллипс
- — параболу
- — гиперболу, — мнимое число
-
—
Наклоне́ние <орбиты> (накло́н <орбиты>, накло́нность <орбиты>) небесного тела — это угол между плоскостью его орбиты и плоскостью отсчёта (базовой плоскостью).
Обычно обозначается буквой i (от англ. inclination). Наклонение измеряется в угловых градусах, минутах и секундах.
- Если , то движение небесного тела называется прямым[6].
- Если , то движение небесного тела называется обратным (ретроградным).
- В применении к Солнечной системе, за плоскость отсчёта обычно выбирают плоскость орбиты Земли (плоскость эклиптики). Плоскости орбит других планет Солнечной системы и Луны отклоняются от плоскости эклиптики лишь на несколько градусов.
- Для искусственных спутников Земли за плоскость отсчёта обычно выбирают плоскость экватора Земли.
- Для спутников других планет Солнечной системы за плоскость отсчёта обычно выбирают плоскость экватора соответствующей планеты.
- Для экзопланет и двойных звёзд за плоскость отсчёта принимают картинную плоскость.
Зная наклонение двух орбит к одной плоскости отсчёта и долготы их восходящих узлов, можно вычислить угол между плоскостями этих двух орбит — их взаимное наклонение, по формуле косинуса угла.
Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемый для математического описания ориентации плоскости орбиты относительно базовой плоскости. Определяет угол в базовой плоскости, образуемый между базовым направлением на нулевую точку и направлением на точку восходящего узла орбиты, в которой орбита пересекает базовую плоскость в направлении с юга на север. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д. Нулевая точка — Первая точка Овна (точка весеннего равноденствия). Угол измеряется от направления на нулевую точку против часовой стрелки.
Восходящий узел обозначается ☊ или Ω.
Формула нахождения долготы восх. узла:
Здесь n — вектор, определяющий восходящий узел.
У орбит с наклоном, равным нулю Ω не определяется (она, как и наклон, равна нулю).
Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты небесного тела), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения небесного тела, обычно выбирается в пределах 0°-360°.
При исследовании экзопланет и двойных звёзд в качестве базовой используют картинную плоскость — плоскость, проходящую через звезду и перпендикулярную лучу наблюдения звезды с Земли. Орбита экзопланеты, в общем случае случайным образом ориентированная относительно наблюдателя, пересекает эту плоскость в двух точках. Точка, где планета пересекает картинную плоскость, приближаясь к наблюдателю, считается восходящим узлом орбиты, а точка, где планета пересекает картинную плоскость, удаляясь от наблюдателя, считается нисходящим узлом. В этом случае аргумент перицентра отсчитывается из притягивающего центра против часовой стрелки.
Обозначается ( ).
Вместо аргумента перицентра часто используется другой угол — долгота перицентра, обозначаемый как . Он определяется как сумма долготы восходящего узла и аргумента перицентра. Это несколько необычный угол, так как он измеряется частично вдоль эклиптики, а частично — вдоль орбитальной плоскости. Однако часто он более практичен, чем аргумент перицентра, так как хорошо определен даже когда наклонение орбиты близко к нулю, когда направление на восходящий узел становится неопределенным[7].
Средняя аномалия для тела, движущегося по невозмущённой орбите — произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом, средняя аномалия есть угловое расстояние от перицентра гипотетического тела, движущегося с постоянной угловой скоростью, равной среднему движению.
Обозначается буквой (от англ. mean anomaly)
В звёздной динамике средняя аномалия вычисляется по следующим формулам:
где:
-
- — средняя аномалия на эпоху ,
- — начальная эпоха,
- — эпоха, на которую производятся вычисления, и
- — среднее движение.
Либо через уравнение Кеплера:
где:
- — эксцентрическая аномалия ( на рис.3),
-
—
- ↑ 1 2 3 4 Ишмухаметова М. Г., Кондратьева Е. Д. Решение задач по небесной механике и астродинамике : Учебно-методическое пособие для практических занятий по дисциплине «Небесная механика». — Казань : Физический факультет Казанского государственного университета, 2009. — 37 с.
- ↑ 1 2 3 С. А. Мирер. Механика космического полета.Орбитальное движение (2013). Дата обращения: 7 июня 2020. Архивировано 23 ноября 2018 года.
- ↑ 1 2 3 Е. И. Бутиков. Закономерности кеплеровых движений : Учебное пособие. — Санкт-Петербург : Санкт-Петербургский государственный университет, 2006. — 61 с.
- ↑ А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, Архивная копия от 8 июля 2020 на Wayback Machine — М.: МЦНМО, 2007. — 136 с.
- ↑ Keplerian Elements Tutorial (англ.). The Radio Amateur Satellite Corporation. Архивировано 14 октября 2002 года.
- ↑ То есть объект движется вокруг Солнца в том же направлении, что и Земля
- ↑ Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner. 6. Celestial Mechanics // Fundamental Astronomy. — 5-е изд. — Springer Science & Business Media, 2007. — С. 117—118.
- Gurfil, Pini (2005). “Euler parameters as nonsingular orbital elements in Near-Equatorial Orbits”. J. Guid. Contrl. Dynamics. 28 (5): 1079—1084. Bibcode:2005JGCD...28.1079G. DOI:10.2514/1.14760.
- Tutorial. AMSAT. Архивировано 14 октября 2002 года.
- Orbits Tutorial. marine.rutgers.edu. Дата обращения: 30 июля 2019. Архивировано 19 апреля 2021 года.