Объём

Объём
${\displaystyle V}$
Размерность	L3
Единицы измерения
СИ	м3
СГС	см3

Воспроизвести медиафайл

Видеоурок: объём

Объём — количественная характеристика пространства, занимаемого телом или веществом. С понятием объёма тесно связано понятие вместимости — объёма внутреннего пространства сосуда, упаковочного ящика и т. п. Объём тела (как и вместимость сосуда) определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей^[1].

Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.

В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.

Математически

Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром ${\displaystyle a}$ вычисляется с помощью выражения ${\displaystyle V=a^{3}}$, а объём прямоугольного параллелепипеда — умножением его длины на ширину и на высоту.

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.

Сводка формул

Форма тела	Формула для вычисления объёма	Обозначения
Куб	${\displaystyle V=a^{3}\;}$
Прямоугольный параллелепипед	${\displaystyle V=abc}$
Призма (B: площадь основания)	${\displaystyle V=Bh}$
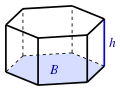
Пирамида (B: площадь основания)	${\displaystyle V={\frac {1}{3}}Bh}$
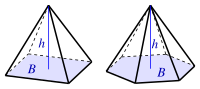
Параллелепипед	${\displaystyle V=abc{\sqrt {K}}}$ ${\displaystyle {\begin{aligned}K=1&+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}}$
Тетраэдр	${\displaystyle V={{\sqrt {2}} \over 12}a^{3}\,}$
Шар	${\displaystyle V={\frac {4}{3}}\pi r^{3}}$
Эллипсоид	${\displaystyle V={\frac {4}{3}}\pi abc}$
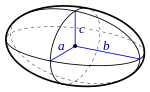
Прямой круговой цилиндр	${\displaystyle V=\pi r^{2}h}$
Конус	${\displaystyle V={\frac {1}{3}}\pi r^{2}h}$
Тело вращения	${\displaystyle V=\pi \cdot \int _{a}^{b}f(x)^{2}\mathrm {d} x}$

Через плотность

Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: ${\displaystyle V={\frac {m}{\rho }}}$.

• 1
  • Ведро = 12,3 литра
  • • 1 пинта = 0,568 литра
    • 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
    • 1 галлон = 8 пинтам = 4,55 литра
    • 1
      • • • Эйфа = 24,883 литра
          • Гин = 1/6 эйфы = 4,147 литра
          • Омер = 1/10 эйфы = 2,4883 литра
          • Кав = 1/3 гина = 1,382 литра

Русские

• Четверик = 26,24 литра (1 пуд зерна)
• Гарнец = 3,28 литра
• Четверть = 1/4 ведра = 3,075 литра
• Штоф = 1/8 ведра = 1,54 литра
• Кружка = 1/10 ведра = 1,23 литра
• Бутылка (винная) = 1/16 ведра = 0,77 литра
• Бутылка (пивная) = 1/20 ведра = 0,61 литра
• Чарка = 1/10 кружки = 0,123 литра
• • 1 бушель = 8 галлонов = 36,36872 литра
  • 1
    • 1 унция (англ.) = 2,841⋅10⁻⁵ м³
    • 1 унция (амер.) = 2,957⋅10⁻⁵ м³
    • 1 кубический дюйм = 1,63871⋅10⁻⁵ м³
    • 1 кубический фут = 2,83168⋅10⁻² м³
    • 1 кубический ярд = 0,76455 м³
    • 1 кубическая астрономическая единица =3,348⋅10²⁴ км³
    • 1 кубический световой год = 8,466⋅10³⁸ км³
    • 1 кубический парсек = 2,938⋅10⁴⁰ км³
    • 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅10⁴⁹ км³

    Примечания

    1. ↑ Математическая энциклопедия, 1982, с. 1149.
    2. ↑ Меры объёма в Древней Руси
    3. ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4

    Литература

    	В Викисловаре есть статья «объём»

    • Объём // Математическая энциклопедия (в 5 томах). — М.:
      • Формулы объёма и программы для расчета объёма (неопр.). Дата обращения: 26 ноября 2020.